STUDIES OF TURBULENT ROTATING CONVECTION

Geophysical Fluid Dynamics Laboratory, Univ. of Colorado

This research is funded by the National Science Foundation, Div. of Physical Meteorology, and NASA, Division of Microgravity Science and Applications.

Experiments in rotating cylindrical containers of fluid are carried to generate data on the structure of thermally heated turbulent motions that are strongly influenced by basic system rotation.  Such rotationally constrained convective flows occur in stars, planetary atmospheres and in the Earth's oceans.  Experimental results are compared with computational simulations of rotating convection by our collaborators:  Joe Werne, Keith Julien and Nic Brummell.  The experiments extend the direct numerical simulation results by going several orders of magnitude higher in Rayleigh number (a measure of thermal forcing) and Taylor number (a measure of system rotation), than can be attained with present computers.

Research Assistant Scott Kittelman with the rotating cell.

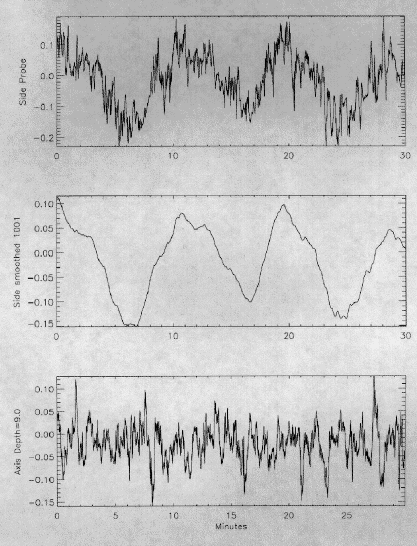
Sketch of the rotating flow.  The heating generates cyclonic plumes.  These interact at moderate rotation levels to produce a mean meridional overturning circulation that  precesses in the anti-cyclonic sense (opposite to the basic rotation Omega).  This precessing cell is most easily detected by comparing temperature time series at the side of the container (at mid-depth), with measurements at the center point (as shown in the above cartoon).

For example, in the precessing mean flow regime, the side probe shows a long period oscillation associated with the successive arrivals of the hot and cold branches of the mean meridional cell.  The high frequency content of these time series is due to convective plumes.

Measurements of the statistics of temperature fluctuations at the center of the cell indicate that if the Rayleigh number is large enough, there is a substantial range of basic rotation over which there is Gaussian behavior associated with lateral mixing by vortices.  At lower thermal forcing exponential statistics are found at all rotation rates.

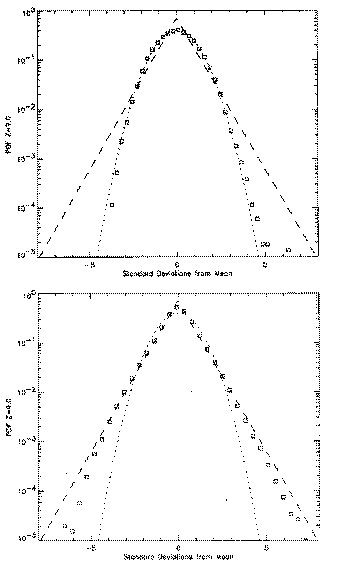
Top:  PDF at Ra = 3*10¹¹ , Ta = 10¹⁰  .  Bottom:   Ra = 3*10¹¹ , Ta = 0 (non-rotating).

At zero Taylor number  [Ta = (2*Omega*H*H/viscosity)^2, where Omega is basic rotation frequency and H is the depth of the cell ], Gaussian statistics are found at large but not extreme values of the Rayleigh number Ra, which measure the strength of the thermal forcing.  At very large Ra and Ta = 0 the statistics are exponential.  As Ta is raised the width of the Gaussian region shrinks, so that at moderately large Ra, exponential statistics are observed for all Ta.  However, as Ra becomes large enough so that the rotating turbulence is very vigorous, the Gaussian region returns.  We have quantified this by measuring the deviation from Gaussian behavior.

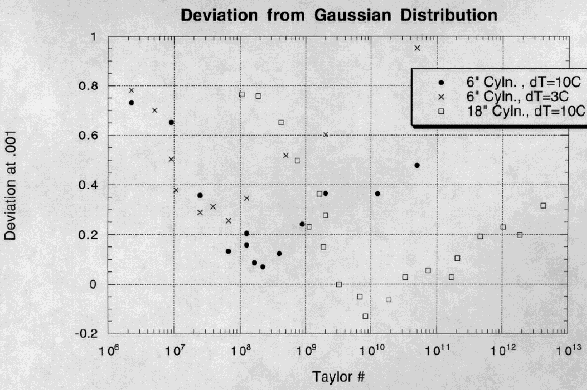
At PDF level 0.001 we fit the data and measure the distance of the curve from Gaussian (0) to exponential (1.0) statistics.  The following plot summarizes the results.

The smallest cylinder with the the weakest imposed temperature difference dT has the lowest Rayleigh number.  The range of Guassian behavior (or equivalently of sub-exponential statistics) is smaller than that for our large cylindrical tank with dT = 10C (in which the Rayleigh number is of order 10^12).

Rapidly rotating experiments are also subject to significant centrifugal buoyancy forces that are not usually included in computational simulations.  One consequence is that the centerpoint temperature is offset by a positive amount.  A model of the effects of centrifugal buoyancy on convection is in agreement with laboratory observations.