INSTABILITY AND TURBULENCE IN A DIFFERENTIALLY-DRIVEN ROTATING CYLINDER

Geophysical Fluid Dynamics Laboratory, Univ. of Colorado

This work  is funded by the National Science Foundation, Div. of Physical Meteorology, and NASA, Division of Microgravity Science and Applications.

In this research we are investigating various aspects of the transition from symmetric states to highly disordered states in a simple system consisting of a rotating cylinder, filled with liquid, with the motion being driven by a differentially rotating contact lid.

This configuration permits investigation of Ekman layer instability, sidewall boundary layer instability, separation of boundary layers on horizontal or vertical walls, axisymmetric and azimuthally wavy instabilities and turbulence.  Because this configuration  is a classic rotating flow system, results from studying it have potential application to a range of natural phenomena including stability of atmospheric vortices and turbulence and instability in ocean gyres. 

Laboratory experiments provide data on the nature of the fundamental instabilities and turbulent states.  These observations are used to validate, motivate, and extend (to higher Reynolds number) computational studies of both the two-dimensional (axisymmetric) and three-dimensional regimes.  The numerical simulations are being carried out by John Lopez of the Mathematics Department at Arizona State University.

Views of an axisymmetric state, looking up from below:

Dye injected from the sidewall spirals inwards (CW looking up from below) by the meridional )or axisymmetric) circulation.  With a counter-rotating driving lid the motion remains circularly symmetric until the lid period (measured relative to the cylinder rotation) is decreased to a critical value.

QT Movie of the circularly stable regime.         Larger Version.

As the differential driving by the top lid becomes faster, various instabilities set in. They are characterized by different wavenumbers that depend on the basic rotation rate of the cylinder.

QT Movie of the 4-wave transition.     Large Version.

As the "supercriticality" (i.e. the degree of forcing by the differentially rotating lid) is increased further, transitions to higher wavenumber and to more complicated states arise.

QT Movie of a high wavenumber state.    Larger Version.

Our ultimate goal is to understand turbulent states and to use laboratory observations as a test for computer simulations that are based on parameterizations of small scale turbulence (the so-called Large Eddy Simulation, or LES models).

QT Movie of a turbulent state (flow visualization by particle suspension).

Data for the critical value of differential rotation required for onset of azimuthal waves in the interior of the flow under counter-rotation of the upper lid.

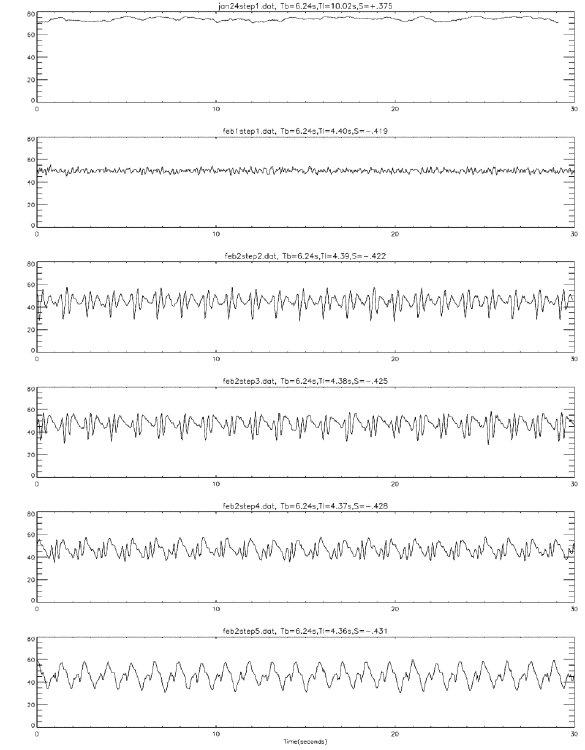
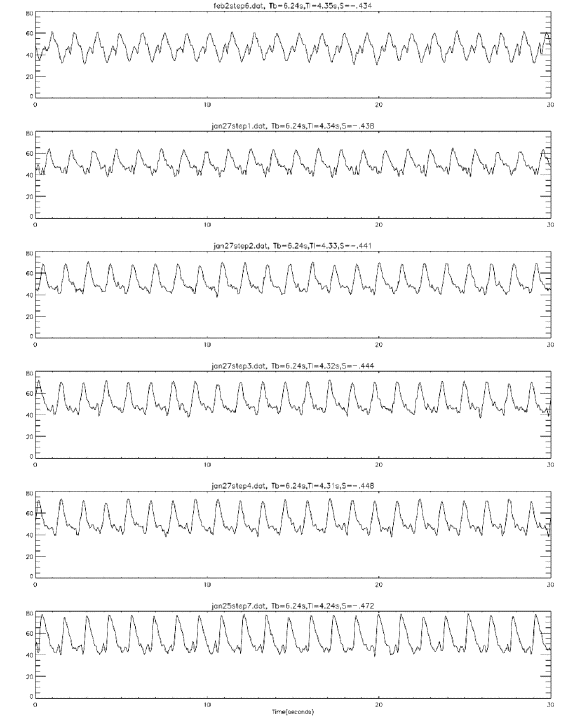
 The Reynolds number is based on the turntable rotation:   Re =  Omega(Base) * R^2/nu,  where Omega is the rotation rate of the turntable, R is the cylinder radius and nu is the viscosity of the fluid (water).  The aspect ration A =  Height/Radius of the cell.  The parameter S measures the forcing and is defined by  S =  Omega(Lid, absolute)/Omega(Base) = 1 + Omega(Lid, relative)/Omega(Base) = 1 + BasePeriod/LidPeriod.  When the differential driving is opposite in direction to that on the base, the lid period is said to be negative.

Shorter Relative Lid Periods (the period of the lid is measured with respect to the body of the cylinder) than those required for the onset of azimuthal waves leads to wavenumber transitions and turbulence as illustrated in the filmclips.

FLOW IN SILICONE OIL  (Re = 1000, A = 0.5):

Observations by Kalliracope (platelet suspension).  A parallel sheet of light illuminated the fluid at mid-depth.  Cameras view the suspension from below and from the side.  The images show the plan-view and a meridional cross-section passing through the axis.  The critical S-parameter, for the transition to wavy motion is 0.420 +- 0.01.  The cricital azimuthal wavenumber is approximately 4.  We extract the luminosity from a point at mid-radius to generate a times series that yields the critical frequency.

Prior to the transition to wavy motion, axisymmetric rings appear and the meridional cross-section shows evidence for multiple axisymmetric cell, perhaps generated by separation of the upper boundary layer.

Time series of intensity vs. S.  Basic rotation period is about 6 seconds.

QT Movie of Stable Motion:  S = -.375  (Plan view on right, Cross-section on left.  The bottom of the tank is the right edge of the cross-section)

QT Movie of Multi-celled Axisymmetric Motion:  S = -.419

QT Movie of Wavy Motion:  S = -.422

QT Movie of Wavy Motion:  S= -.425

QT Movie of Irregular Motion: S = -.625

QT Movie of Turbulent Motion:  S = -.971

Time series for supercritical states.  Luminosity at r ~ 0.5.