CONVECTION IN A ROTATING SHEAR FLOW:  A POSSIBLE MECHANISM FOR VORTEX EYES

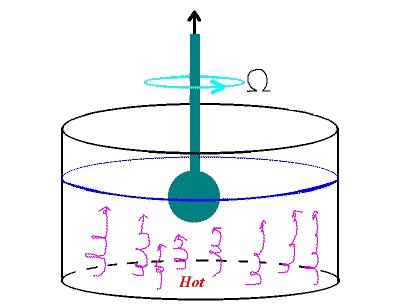
Geophysical Fluid Dynamics Laboratory, Univ. of Colorado

This research is funded by the National Science Foundation, Div. of Physical Meteorology.

In this work we are interested in the effect of a lateral shear flow V(r), where V is the velocity in the azimuthal direction and r is the radius on thermal convection driven by heating from below.  We are interested in establishing that conditions under which a swirling vortex flow can significantly modify the structure of convection in a rotating system.  Examples of such interactions in nature arise in the eye region of hurricanes and in island vortices which form over warm water that stimulates relatively weak convection throughout out the system.  A sketch of our laboratory model of shear interaction with rotating convection is shown below.

A cylinder half filled with water is rotated at rate Omega.  When a sphere, initially sitting at mid-depth at the top of the fluid, is withdrawn vertically, a vortical flow is generated by vortex stretching in the area subtended by the sphere.  Before the sphere is withdrawn, thermal convection is set up by heating the bottom of the tank.  Under suitable external conditions (large enough Omega, weak enough convection), the vortex entirely wipes out the convection occurring under it.

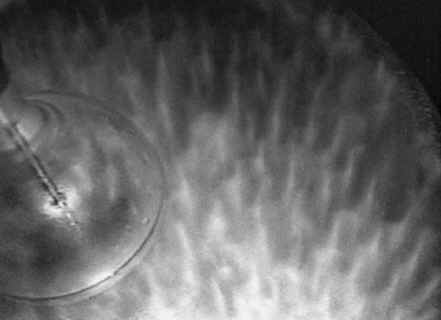
Photograph of the experiment.

Convection (visualized by Kalliroscopic platelets in the water), with the sphere half immersed.

Convection field after the sphere has been withdrawn.  Note the absence of plumes in the fluid (now with differential rotation V(r) ) where the sphere had been.

QT Movie of the Vortex Forming as the Cylinder is Withdrawn (visualization by thymol dye)

QT Movie Of  The Withdrawal  (visualization by Kallirocope)

In this research we are carrying out linear and nonlinear stability theory (to ascertain the parametric dependence of the stabilization), laboratory experiments (to investigate parameter regions not accessible to theory), and computational simulations (to quantify the detailed mechanical and thermal processes leading to linear and nonlinear stabilization).  Applications to atmospheric convection in strong vortices, and to ocean convection in Gulf Stream Rings and sheared Gulf Stream  currents , V(x) or U(y) are being considered.